引言
不同规范里参数大都相似
世界上有近200个国家和地区,几乎每个国家都有自己的荷载规范,不同的荷载规范,其计算过程也多种多样。世界上的这些规范看似系数取名不同,公式字母不一样,但是却都遵循相同的规律,之前讲过,对于任何国家的荷载规范,风荷载的计算方式基本上是一致的,万变不离其宗,都是如下公式的变形。
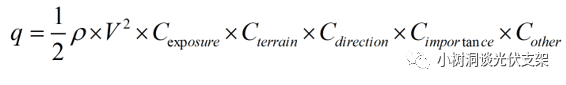
▵风荷载计算基本公式
接下来,我们对各个参数依次和风洞测试进行对照。
风有两种比较重要的参数,一个是“重现期”,公众号之前《千年一遇?台风是要成精了》系列已经有所介绍。另外一个就是“时距”,目前世界上风荷载规范主要有三种风速时距,3s阵风风速,10分钟平均风速,1小时平均风速。这三种风速大小可以互相进行转换。
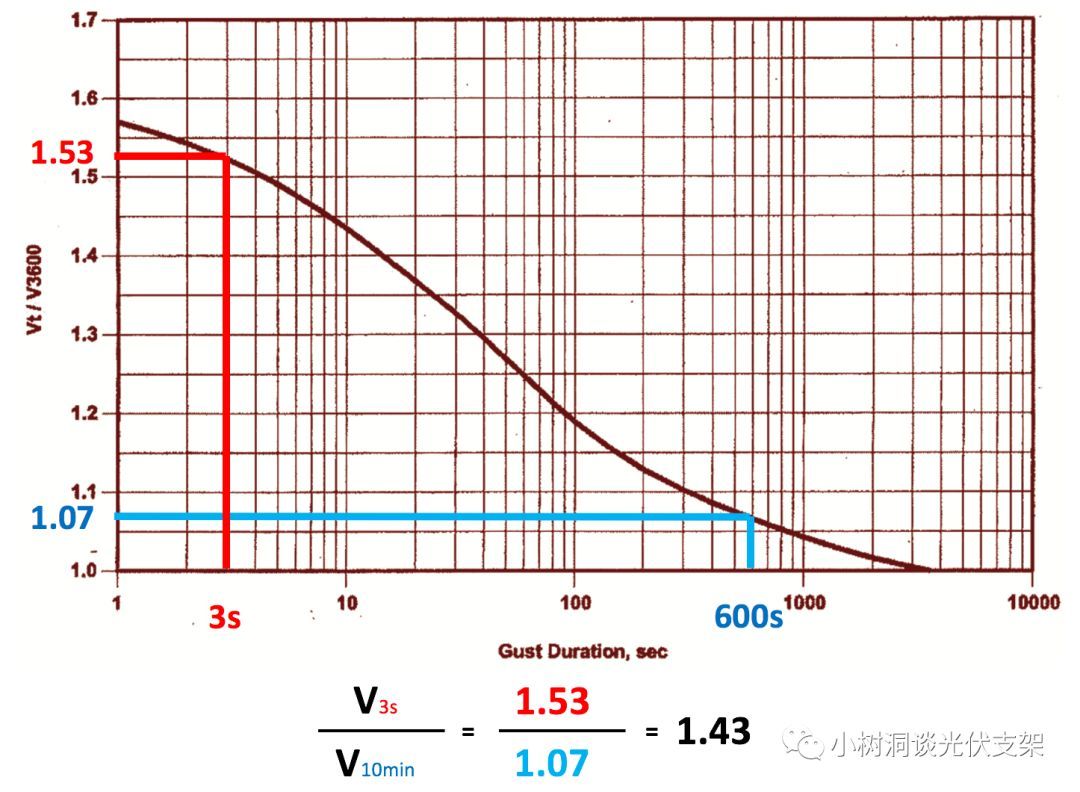
▵美标提供的时距转换曲线(Durst Curve)
我们知道对于自然风而言,它是由两种类型的风荷载组成的:
周期较长的平均风荷载
周期较短的脉动风荷载
其中平均风荷载可类比为一种静态的力,而脉动风荷载因为其具有随机性,情况比较复杂。1967年,著名的风工程科学家-Davenport提出了一种方法来简化这种脉动风荷载的计算,称之为GLF(Gust Loading Factors),简单的来说就是在静态力上再乘以一个大于1的系数(阵风系数或风振系数)来拟真这类脉动风荷载。
而对于脉动风荷载来说,又有两种分量需要考虑:
背景分量,考虑风速的瞬时变化,阵风系数
振动分量,考虑结构的振动响应,动态放大系数
我们知道,国标GB50009在计算风荷载时有两种方法供选择:
计算主要受力结构时,考虑风振系数
计算围护结构时,考虑阵风系数
这里的阵风系数仅仅考虑了背景分量,适用于刚性较强的结构。而风振系数既考虑了风的背景分量,也考虑了结构振动的响应,适用于刚性较弱的结构。
对于基本频率较高的部分固定支架和屋顶支架,仅考虑阵风系数即可,可以按照围护结构进行设计。
对于跟踪器这种风致敏感的结构,则需要考虑结构本身的振动对荷载的放大效应,需要考虑风振系数,应该按照主要受力结构进行设计。
如前面所述,当结构刚性较强时,则不需要考虑结构的振动响应,而只需要考虑风速的瞬时变化产生的效果,那么这时就只要在平均风荷载上(国标,欧标,日标都为10分钟平均风荷载)乘以一个阵风系数(Gust Factor)即可。
下面我们就分别用美标和欧标来进行详细讲解:
▵美标的3秒阵风风速为40m/s左右
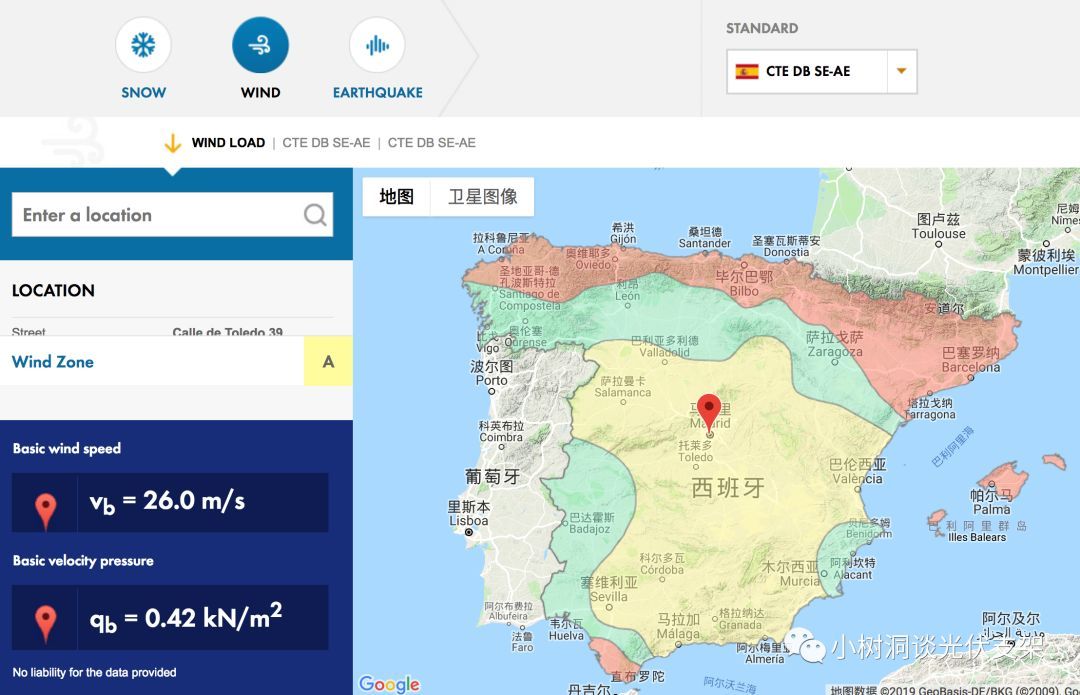
▵欧标的10分钟风速为30m/s左右
阵风系数是指瞬时风荷载(或风速)相较于平均风荷载(或风速)的比值。而随着高度的增大,脉动风荷载的效应降低,阵风系数也相应的减少。
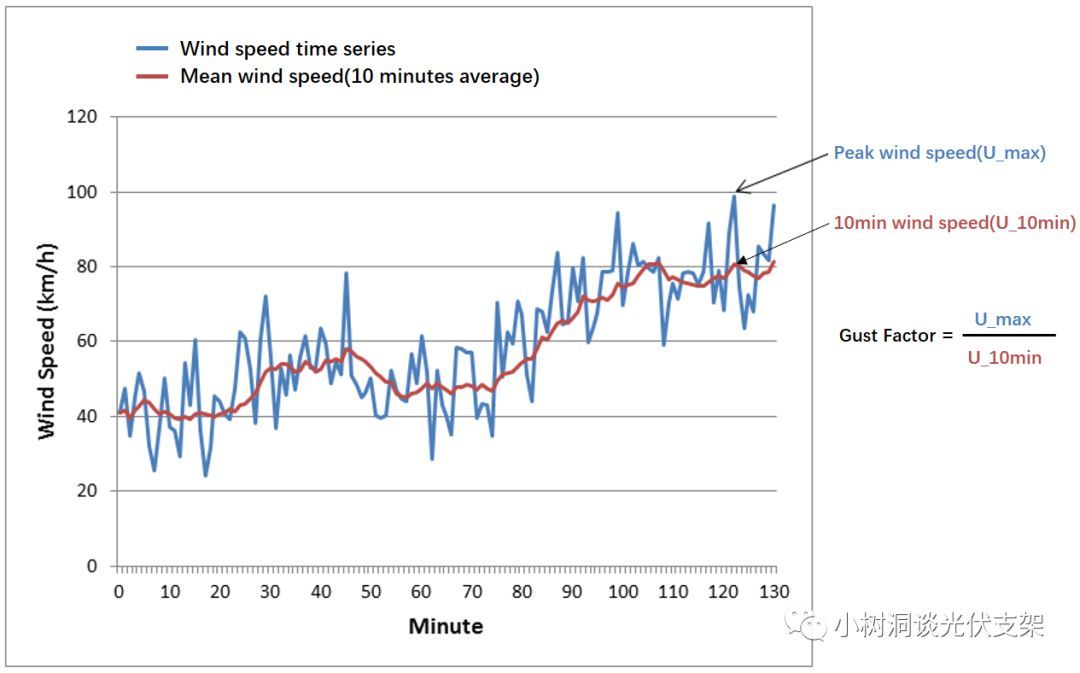
▵阵风系数的计算图例
▵阵风系数随高度的增加而递减(来源:WMO)
通常我们把3秒的瞬时风速称之为3秒阵风风速(3s gust wind speed),对于欧标来说,系数Exposure Factor-Ce(z)就是将10分钟的风速转换成了3s阵风风速。所以这个Ce(z)也就是我们所说的阵风系数。
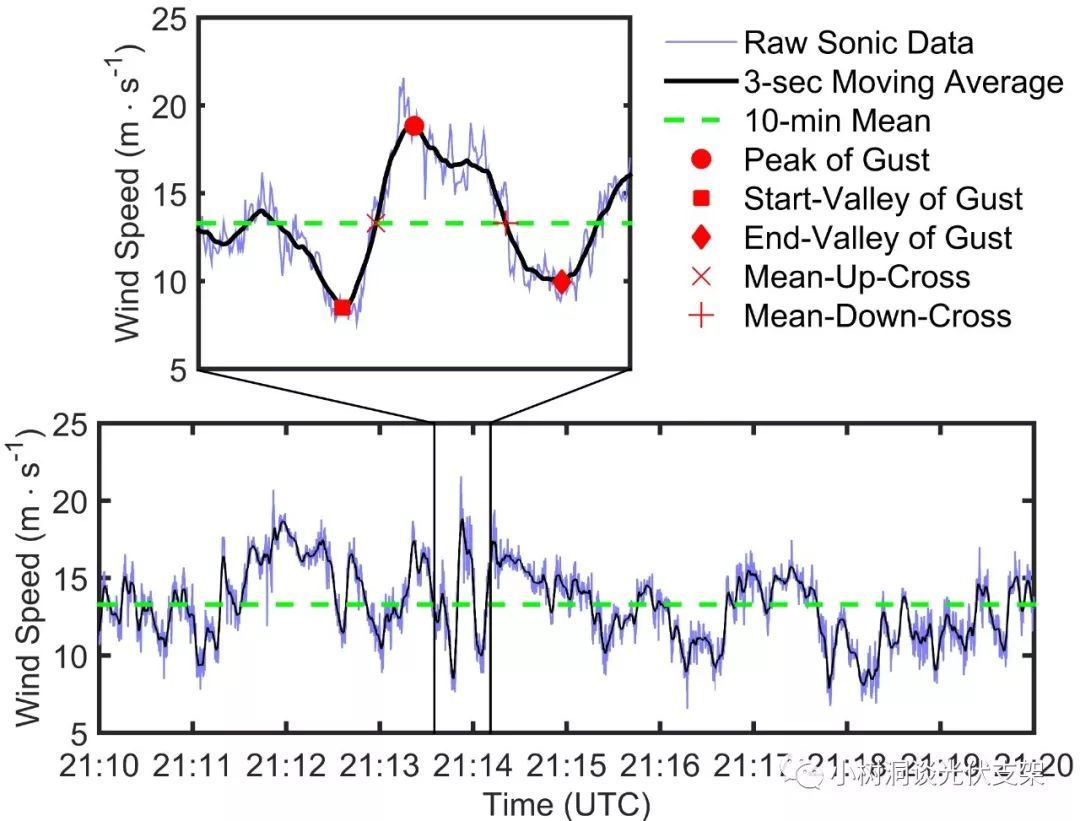
▵10分钟风速(绿虚线)与
3s阵风风速(黑实线)的关系
对于美标,尽管也有Gust Factor-G,但是这个G并不是我们常说的阵风因子,而是考虑了风速瞬时作用到结构面积比较大的建筑物上时,建筑物上各个区域的风压并不是瞬间都是相同的,实际风压会有折减,因此对于大型建筑物,这里G是取0.85。而对于跟踪器,因为其有效特征长度都在2~4米左右,结构比较“小”,瞬间的风压可以看成是相同的,所以在计算时应该取1.0。在进行风洞测试时,往往将G和CN(也就是压力系数Cp)合并在一起,取做GCN。
▵欧标/美标/加标
三种不同时距风速规范的计算对比
当我们找到每个规范里面的阵风因子后,不管是10分钟风速的欧标、3s阵风的美标,还是1小时平均风速的加标,就可以使用同一套3s阵风下的风洞系数了。
前面所讲的“阵风系数”,主要针对的是刚性较强的结构,对于像跟踪系统这样刚性较弱的结构,还需要考虑其结构振动所带来的额外风荷载,也就是我们说的“风振系数”。
对于国标来说,风振系数既包括了单纯的瞬时变化的脉动风荷载,又包含了结构的动态响应。但是对于使用3秒阵风的规范,例如美标,只需要考虑结构的动态响应即可,这时需要乘上的系数则称之为“动态放大系数-DAF(Dynamic Amplificaiton Factor)“。
对于同一个角度,同一种设计的跟踪系统,影响DAF这种系数的主要有以下几点:
风速越大,DAF越大
结构频率越小,DAF越大
结构阻尼比越小,DAF越大
对于跟踪器来说,DAF数值的大小有时甚至可以到达5.0,也就是说实际考虑了风致共振后的荷载是静态风荷载的5倍。
前面第一篇的时候,小树洞介绍了一个重要的概念“大气边界层”,在这个边界层上,风速随着高度的增大而增大,也就是说,在高层建筑物的不同高度区域,他们受到的风速是不一样的。

▵大气边界层内
风速随高度增大而增大
当我们希望计算不同高度的风速时,则需要乘上一个系数,称为风压高度变化系数(height factor),于是不同高度的风速“V”和其高度“z“组成了一个函数,表现在坐标系上则是一个风速随高度变化的曲线。目前世界上主要使用三种函数来拟合这条曲线:
- 幂函数率,Power Law
- 对数率,Logarithmic Law
- Deaves&Harris模型
▵三种大气边界层拟合函数率
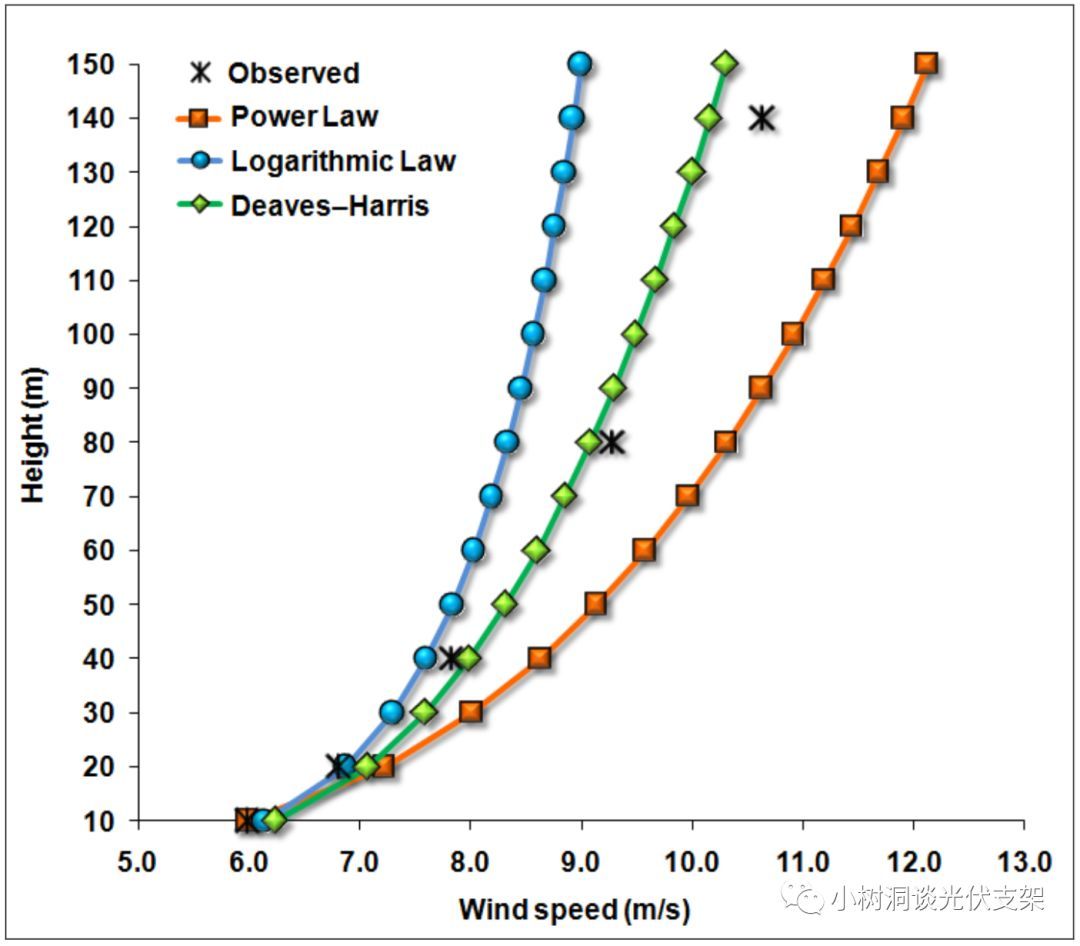
▵三种函数率在高层建筑中的拟合对比
目前小树洞遇到的规范主要使用幂函数率和对数率两种,而它们在低矮建筑物的区别几乎可以忽略。
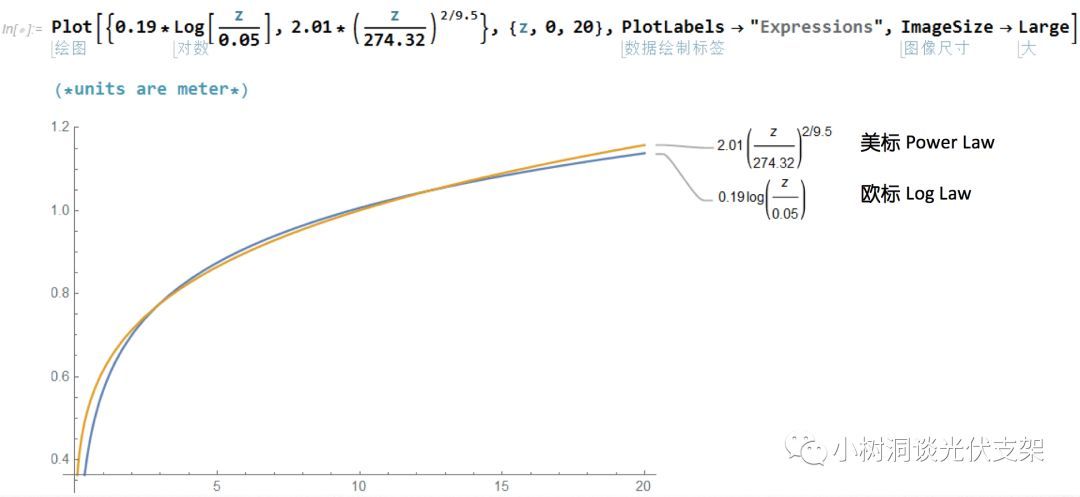
▵小树洞拟合的
美标幂函数率和欧标对数率
我们常说某地最大风速30m/s,既然风速在不同高度上的值不相同,那么为什么对于一个城市或者区域我们却只考虑一个风速值呢?如果我们翻看下各国的风荷载规范,会发现一个很有意思的现象:

▵美标ASCE 7-10
9.1m高度时系数为0.98
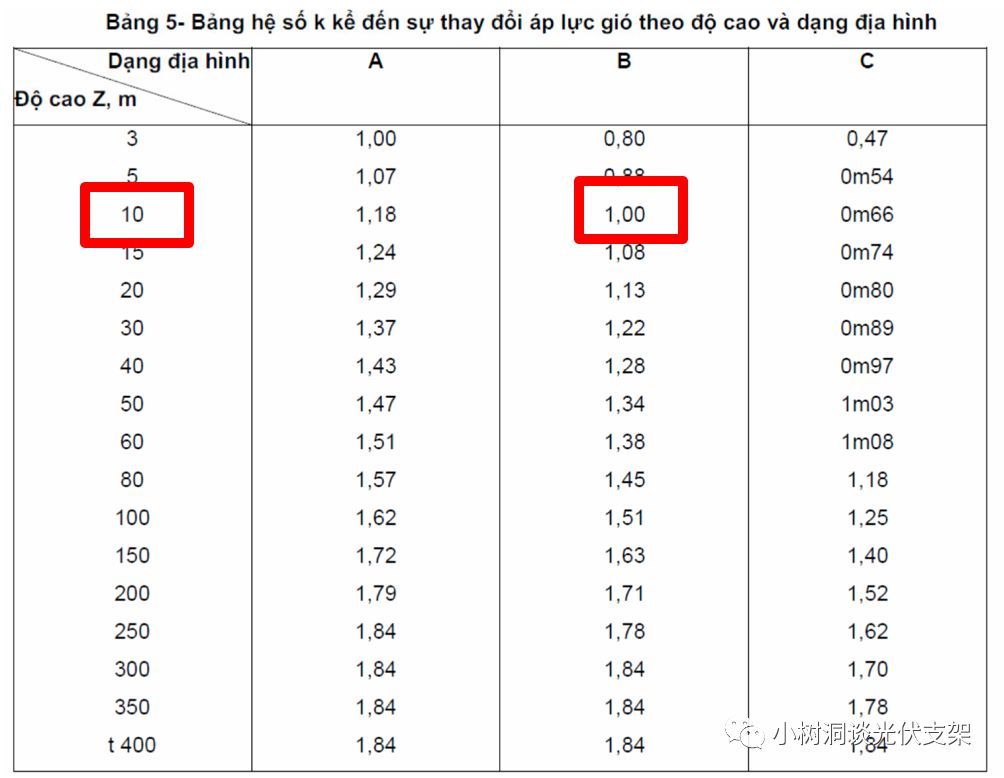
▵越南标准TCVN 2737
10m高度时系数为1.00
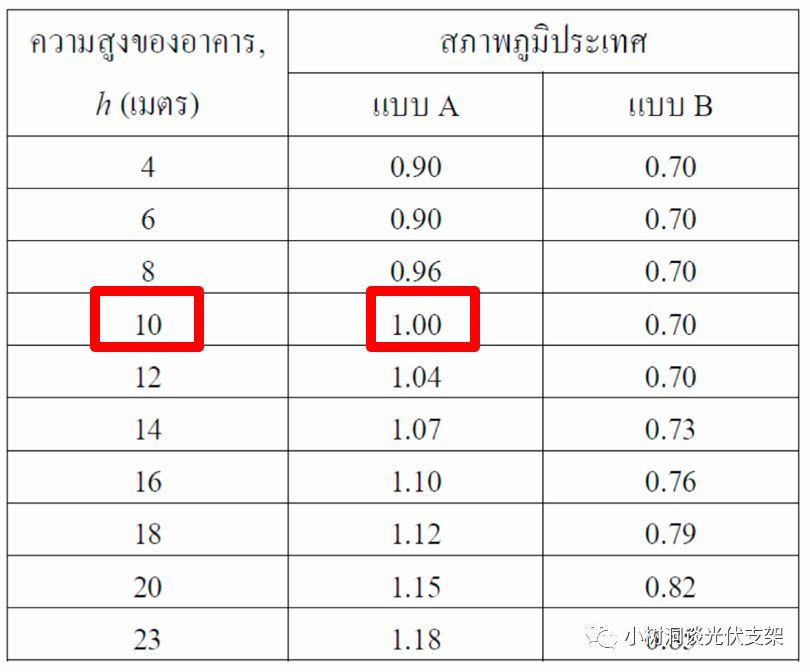
▵泰国标准DPT 1311-50
10m高度时系数为1.00
几乎所有荷载规范的风压高度变化系数,在开阔地形10m高度上的值都非常接近1.0,也就是在这种地形的10m高处,我们的计算风压不需要根据高度进行折减或增加。所以我们常说的风速其实叫做“参考风速(reference velocity)”,而参考风速都是在开阔地形,10m高度上的速度值。这里要注意的是,大部分的风洞系数所参考的已经是10m高度的风速了,所以在使用这类风洞系数时,风压高度变化系数无需折减,应该取1.0。

▵跟踪器大多建设在
地面无遮挡的开阔地形上
一个地方的风向不可能每时每刻360度都是相同的,比如杭州冬天吹西北风,夏天吹东南风,这两个方向的风往往最强,有时候根据已有的气象资料,我们可以分析出各个方向风速的概率分布。
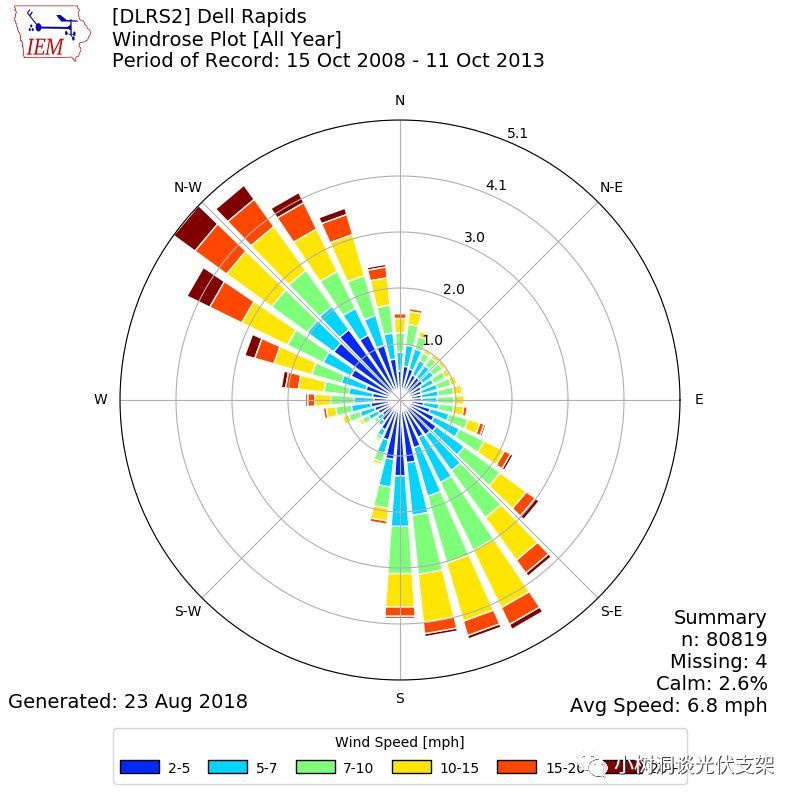
▵风向玫瑰图
对于风洞测试,由于每隔5度或者10度都会进行一次吹风模拟,所以风的风向可以不用考虑。也就是说,每个方向都是最大风速。这样的话运用到任何地方,都会比较保守。
▵风洞360°吹风测试
(来源:SunAction Tracker)
很多规范里都有条文规定,如果坡度小于3°,则不需要考虑地形坡度对风速的影响,如果坡度大于3°,那么就需要进行额外的分析。
The effects of orography may be neglected when the average slope of the upwind terrain is less than 3°.
-Eurocode 1991-4
The effect of topography shall be significant at a site when the upwind slope is more than about 3°, and below that, the value of k3 may be taken to be equal to 1.0.
-Indian Standard(IS 875)
这里多说几句,由于大坡度会对大气边界层造成“挤压”,也就是在山顶和山腰,风速会有非常大的“突跃(Speed Up)”,小树洞也曾专门做过这方面的研究,在山顶上或者山腰的风压,与平地的风压比较,会有1.5~3倍的增大。理论上这些地区是不适合建设跟踪器甚至固定支架项目的。
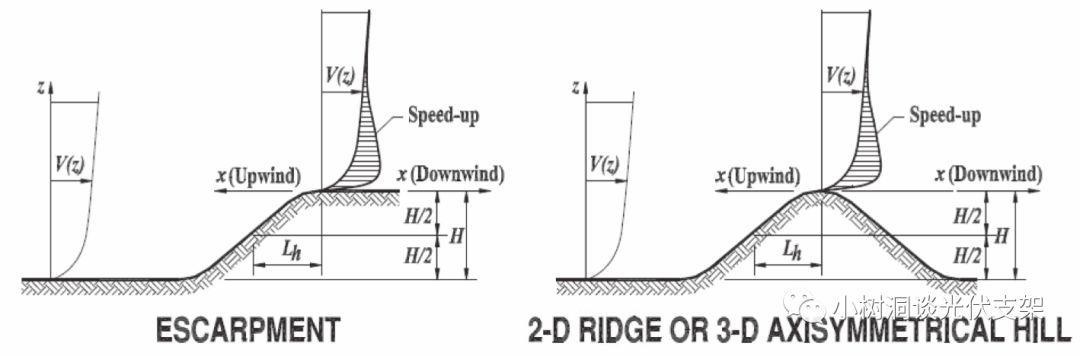
▵美标ASCE 7对地型系数的定义
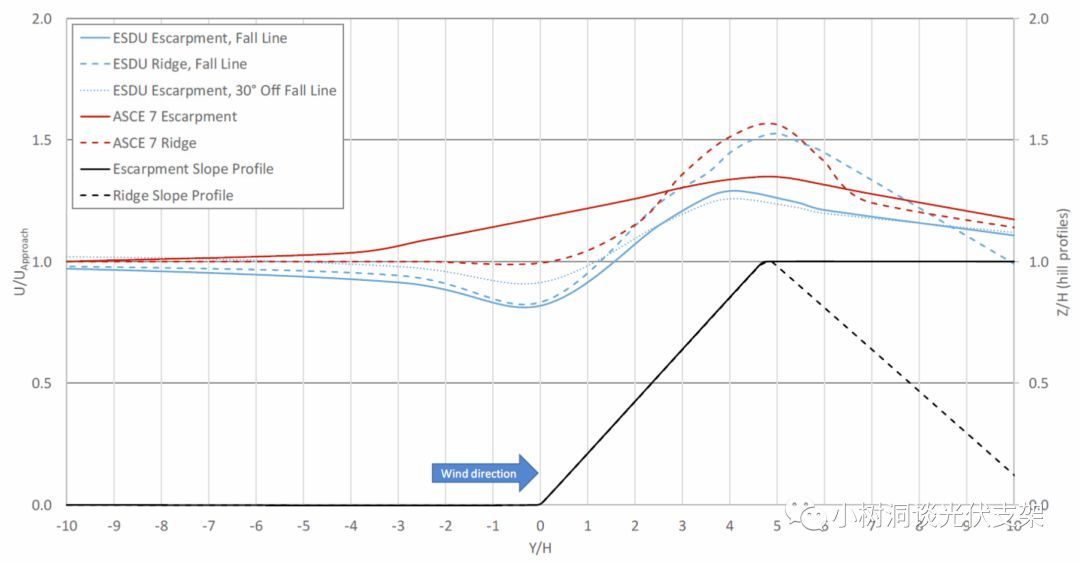
▵风在山区或陡壁上会有
1.2到1.6倍的速度增量
(来源:ESDU E0108)

▵不仅风压在斜坡上会增大
雪也会在斜坡上产生累积效应

▵相同道理
沙尘也会在斜坡上积累
但凡是做国际跟踪器项目,都必须使用当地荷载和钢构规范进行钢结构的分析和计算,小树洞曾研究超过30个国家的原版风荷载、雪荷载、地震荷载、甚至洪水和冰冻荷载规范。这些规范看似千变万化,但是每一个公式都具有很相似的意义和取值方式。
不管是英语、德语、西班牙语、意大利语,还是越南语、泰语、阿拉伯语、缅甸语、日语。当掌握了荷载规范制定的规律后,就会发现,只要了解每一个参数是如何选择的,就可以计算对应风速下的荷载,这样的话,那些文字和语言反而倒是次要的了。很多规范其实都是相通的,熟悉其中一种就可以在短时间内快速掌握相同类型规范,融会贯通。
世界上的主要荷载规范无非就下面四大体系:
- 欧标 Eurocode 1991
- 美标 ASCE 7
- 澳标 AS 1170
- 英标 BS 6399
只要熟读这四种规范,掌握他们所有系数的计算方式和取值原理,就能大幅度提升对其他规范的学习速度和效率。
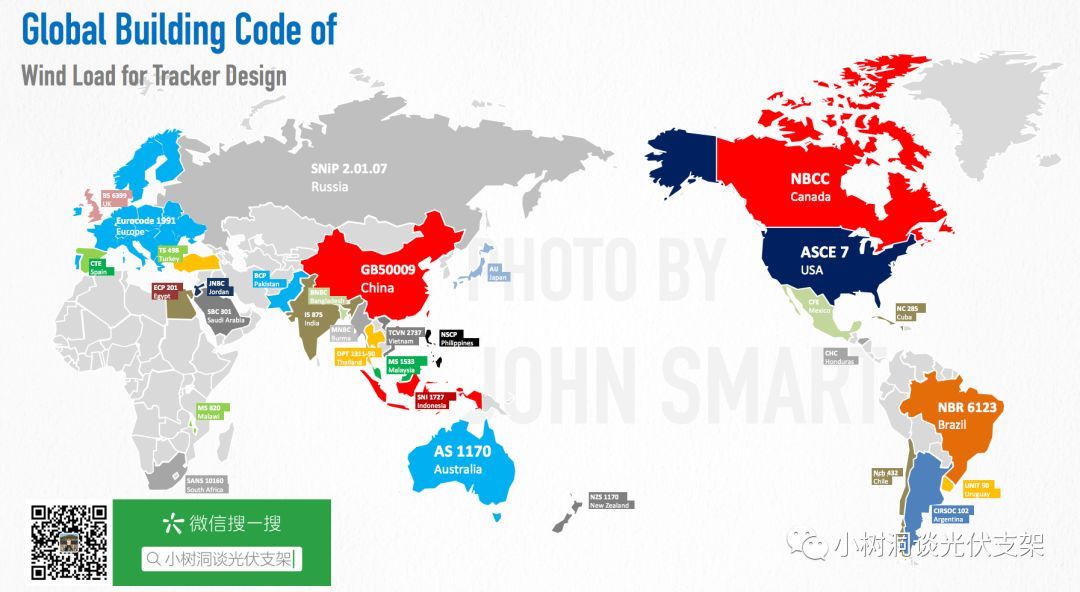
▵小树洞整理全球主要国家荷载规范
关注小树洞
做个有料的
光伏工程师